MPSK通信系统的设计与性能研究
|字数总计:2.9k|阅读时长:11分钟|阅读量:
[noway]建议不要直接抄[/noway]
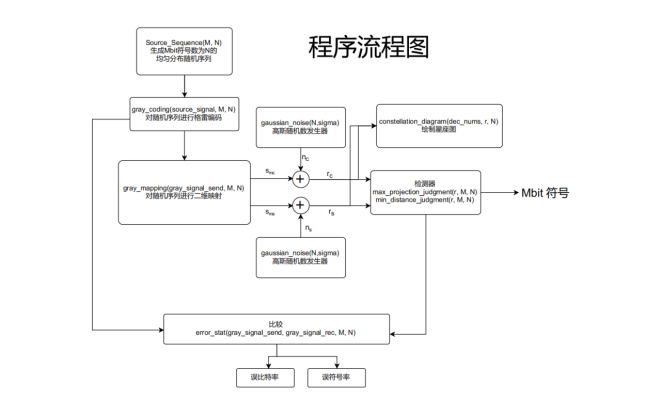
系统实现流程图
子函数
1. 信源序列生成子函数
输入:M为码元位数,N为符号长度。
输出:1行,N列的取值范围为[0,7]的矩阵。
方法:利用randi([0, 2^M-1], 1, N)函数产生1行,N列的取值范围为[0,7]的矩阵。
1
2
3
4
5
| function sourse_signal = generate_Source(M, N)
sourse_signal = randi([0, 2^M-1], 1, N);
end
|
2. Mbit格雷码表子函数
输入:M为码元位数。
输出:Mbit 的格雷码对照表(M行,2^M列的0,1矩阵)。
方法:对[1,2^M]进行遍历:通过dec2bin()、double()和boolean()函数将十进制数转为二进制数,再通过二进制数转格雷码规律将自然二进制数转为格雷码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| function gray_table = Gray_Table(M)
gray_table = zeros(M, 2^M);
for i = 1 : 2^M
bin_str = dec2bin(i-1, M);
bin_num = double(boolean(bin_str-'0'));
for j = 1 : M
if j == 1
gray_table(j, i) = bin_num(j);
else
gray_table(j, i) = xor(bin_num(j-1), bin_num(j));
end
end
end
end
|
3. 信源符号序列格雷编码子函数
输入:source_signal为产生的信源符号序列,M为码元位数,N为符号长度。
输出:M行,N列的0,1矩阵。
方法:通过自己编写好的的Mbit 格雷码表生成函数Gray_Table(M)生成格雷码表,将序列的符号值+1作为索引,得到符号对应的格雷码。
1
2
3
4
5
6
7
8
9
| function gray_signal = code_Gray(source_signal, M, N)
gray_signal = zeros(M, N);
gray_table = Gray_Table(M);
for i = 1 : N
gray_signal(:,i) = gray_table(:,source_signal(i)+1);
end
end
|
4. 格雷码映射子函数
输入:gray_signal为经过格雷编码的信源序列,M为码元位数,N为符号长度。
输出:dec_nums为格雷码解码得到的符号序列,mapping_signal为2行,N列的坐标矩阵。
方法:现将之前得到格雷编码的信源序列解码为自然二进制数,再转为十进制数,通过正交基投影得到星座图坐标矩阵。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| function [dec_nums, mapping_signal] = map_Gray(gray_signal, M, N)
mapping_signal = zeros(2, N);
temp = zeros(M, N);
dec_nums = zeros(1, N);
for i = 1 : N
for j = 1 : M
if j == 1
temp(j, i) = gray_signal(j, i);
elseif j == 2
temp(j, i) = xor(gray_signal(j-1, i), gray_signal(j, i));
else
temp(j, i) = xor(temp(j-1, i), gray_signal(j, i));
end
end
end
for i = 1 : N
for j = 1 : M
dec_nums(i) = dec_nums(i) + temp(j, i) * 2^(M - j);
end
end
for i = 1 : N
mapping_signal(1, i) = cos(dec_nums(i)*pi/(2^(M-1)));
mapping_signal(2, i) = sin(dec_nums(i)*pi/(2^(M-1)));
end
|
5. 噪声序列生成子函数
输入:N为符号长度,噪声方差sigma
输出:2行,N列的矩阵
方法:通过噪声方差,计算得出两路正交的零均值高斯噪声序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
function noise = generate_Noise(N, sigma)
nc = zeros(1, N);
ns = zeros(1, N);
for i = 1 : N
u = rand;
z = sigma*sqrt(2 * log(1 / (1 - u)));
u = rand;
nc(i) = z * cos(2 * pi * u);
ns(i) = z * sin(2 * pi * u);
end
noise(1,:) = nc;
noise(2,:) = ns;
end
|
6. MPSK的零方差噪声信号星座图生成子函数
输入:M为码元位数
输出:MPSK 的零方差噪声信号星座图(2行,2^M列的矩阵)
方法:对[1,2^M]进行遍历:通过正交基完成在星座图上的投影
1
2
3
4
5
6
7
| function constellation_table = Constellation_Table(M)
constellation_table = zeros(2,2^M);
for i = 1 : 2^M
constellation_table(1, i) = cos((i-1)*pi/(2^(M-1)));
constellation_table(2, i) = sin((i-1)*pi/(2^(M-1)));
end
end
|
7. 星座图生成子函数
输入:dec_nums为之前解码时得到的信源的符号序列,r为接收信号,N为码元个数
方法:通过dec_nums和r的对照关系,将相同符号的接收序列映射为同一颜色,r的第1行作为x坐标,第2行作为y坐标,使用plot绘制星座图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function draw_Constellation(dec_nums, r, N)
figure("name", "星座图")
color = 'rybgkcmg';
for i = 1 : N
plot(r(1, i), r(2, i), "*", 'Color', color(dec_nums(i)+1));
hold on;
end
hold off
axis([-2, 2, -2, 2])
line([-2, 2], [0, 0] , "color", "red")
line([0, 0], [2, -2], "color", "red")
title("星座图")
end
|
8. 最大投影准则判决子函数
输入:r为接收信号,M为码元位数,N为符号长度。
输出:M行,N列的0,1矩阵(判决得到的是信号的格雷编码)。
方法:通过先前编写好的Gray_Table(M)和Constellation_Table(M)函数,生成Mbit 格雷码对照表和MPSK的零方差噪声信号星座图,遍历r每一列与零方差噪声信号星座图矩阵的每一列的投影,得到的最大投影对应的零方差噪声信号星座的索引,通过索引判断序列对应的符号,最后对判决得到的索引从格雷码表中得到序列对应的格雷码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| function c = judge_Max_Projection(r, M, N)
gray_table = Gray_Table(M);
constellation_table = Constellation_Table(M);
d = zeros(1, 2^M);
c = zeros(M, N);
for i = 1 : N
for j = 1 : 2^M
d(j) = constellation_table(:,j)' * r(:,i);
end
[~,m] = max(d);
c(:,i) = gray_table(:,m);
end
end
|
9. 最小距离准则判决子函数
输入:r为接收信号,M为码元位数,N为符号长度
输出:M行,N列的0,1矩阵(判决得到的是信号的格雷编码)
方法:通过先前编写好的Gray_Table(M)和Constellation_Table(M)函数,生成Mbit 格雷码对照表和MPSK的零方差噪声信号星座图,遍历r每一列与零方差噪声信号星座图每一坐标的距离,得到的最小距离对应的零方差噪声信号星座的索引,通过索引判断序列对应的符号,最后对判决得到的索引从格雷码表中得到序列对应的格雷码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| function c = judge_Min_Distance(r, M, N)
gray_table = Gray_Table(M);
constellation_table = Constellation_Table(M);
d = zeros(1, 2^M);
c = zeros(M, N);
for i = 1 : N
for j = 1 : 2^M
d(j) = (r(1,i) - constellation_table(1,j))^2 + (r(2,i) - constellation_table(2,j))^2;
end
[~,m] = min(d);
c(:,i) = gray_table(:,m);
end
end
|
10. 误比特率和误符号率统计子函数
输入:gray_signal为发送信号的格雷码,gray_signal_rec为判决输出信号的格雷码,M为码元位数,符号长度为N
输出:error_bits_rat为误比特率,error_sym_rat为误符号率
方法:通过对发射端的序列格雷码与接收端判决后的序列格雷码遍历,判断相同位置的比特是否相同,如果不同,则误比特数+1,若在一个符号内出现误比特,则误符号数+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| function [error_bits_rat, error_syms_rat] = stat_Error(gray_signal, gray_signal_rec, M, N)
error_bits = 0;
error_syms = 0;
symbol = 0;
for i = 1 : N
for j = 1 : M
if ~isequal(gray_signal(j, i), gray_signal_rec(j, i))
error_bits = error_bits + 1;
symbol = 1;
end
end
if symbol == 1
error_syms = error_syms + 1;
symbol = 0;
end
end
error_bits_rat = error_bits/(M*N);
error_syms_rat = error_syms/N;
end
|
测试脚本(主程序)
1. 星座图测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| N = 1000;
M = 2;
source_signal = generate_Source(M, N);
gray_signal_send = code_Gray(source_signal, M, N);
[dec_nums, mapping_signal] = map_Gray(gray_signal_send, M, N);
sigma = 0.8;
noise = generate_Noise(N,sigma);
r = mapping_signal + noise;
draw_Constellation(dec_nums, r, N);
gray_signal_rec = judge_Min_Distance(r, M, N);
|
2. 误比特率和误码率测试主程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| close all;
clear;
clc;
N = 100000;
M = 2;
Eb = 1/M;
xlen = 16;
SNR = zeros(1, xlen);
error_bits_rat = zeros(1, xlen);
error_bits_the = zeros(1, xlen);
error_syms_rat = zeros(1, xlen);
error_syms_the = zeros(1, xlen);
sigma = zeros(1, xlen);
for i = 1:xlen
SNR(i) = i - 6;
N0 = Eb/(10^(SNR(i)/10));
sigma(i) = sqrt(N0/2);
source_signal = generate_Source(M, N);
gray_signal_send = code_Gray(source_signal, M, N);
[dec_nums, mapping_signal] = map_Gray(gray_signal_send, M, N);
noise = generate_Noise(N,sigma(i));
r = mapping_signal + noise;
gray_signal_rec = judge_Max_Projection(r, M, N);
[error_bits_rat(i), error_syms_rat(i)] = stat_Error(gray_signal_send, gray_signal_rec, M, N);
error_bits_the(i) = 0.5*erfc(sqrt(Eb/N0));
error_syms_the(i) = 2 * error_bits_the(i) * (1 - 0.5 * error_bits_the(i));
end
M = 3;
Eb = 1/M;
error_syms_rat8 = zeros(1, 15);
error_syms_the8 = zeros(1, 15);
for i = 1 : xlen
N0=Eb/(10^(SNR(i)/10));
sigma(i)=sqrt(N0/2);
source_signal =generate_Source(M, N);
gray_signal_send = code_Gray(source_signal, M, N);
[~, mapping_signal] = map_Gray(gray_signal_send, M, N);
noise = generate_Noise(N,sigma(i));
r = mapping_signal + noise;
gray_signal_rec = judge_Max_Projection(r, M, N);
[~, error_syms_rat8(i)] = stat_Error(gray_signal_send, gray_signal_rec, M, N);
error_syms_the8(i) = erfc(sqrt(log2(2^M)*Eb/N0) * sin(pi/(2^M)));
end
figure('name', 'error_bits');
semilogy(SNR, error_bits_rat, 'r-x');
hold on;
semilogy(SNR, error_bits_the, 'r-o');
grid on
xlabel('Eb/N0(dB)');
ylabel('误比特率') ;
title('QPSK通信系统的误比特率');
hold off;
legend({'QPSK仿真误比特率', 'QPSK理论误比特率'},'Location', 'southwest')
figure('name', 'error_syms');
semilogy(SNR, error_syms_rat, 'g-x');
hold on;
semilogy(SNR, error_syms_the, 'g-o');
semilogy(SNR, error_syms_rat8, 'r-x');
semilogy(SNR, error_syms_the8, 'r-o');
xlabel('Eb/N0(dB)');
ylabel('误符号率') ;
title('QPSK和8PSK通信系统的误符号率比较');
hold off;
legend({'QPSK仿真误符号率', 'QPSK理论误符号率', '8PSK仿真误符号率', '8PSK理论误符号率'},'Location', 'southwest')
|

