image-20220210231947937

第1题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
clear all;
clc;
%为了减少DFT的点数，需采用基-2FFT算法，根据题目所述可知，只需要一次分解即可
N = 64;
n = 0:2*N-1;
k = 0:N-1;
n1 = 2*k;
n2 = 2*k+1;
W2Nk = exp(-1i*2*pi*k/2/N);
xn = cos(2*pi*7*n/N)+cos(2*pi*19*n/N)/2;    %原序列
x1n = cos(2*pi*7*n1/N)+cos(2*pi*19*n1/N)/2; %原序列的偶项
x2n = cos(2*pi*7*n2/N)+cos(2*pi*19*n2/N)/2; %原序列的奇项
X1k = fft(x1n,N);   %x1n的N点DFT
X2k = fft(x2n,N);   %x2n的N点DFT
Xkfront = X1k + W2Nk.*X2k;
Xklatter = X1k - W2Nk.*X2k;
Xk = [Xkfront,Xklatter];
subplot(2,1,1);
stem(n,abs(Xk));
xlabel("k");
ylabel("幅值");
title("基2-FFT的64点FFT算法");
grid on;

%对序列直接进行128点DFT作为理论分析与对比
XkDFT = fft(xn,2*N);
subplot(2,1,2);
stem(n,abs(XkDFT));
xlabel("k");
ylabel("幅值");
title("128点DFT算法");
grid on;

输出结果：

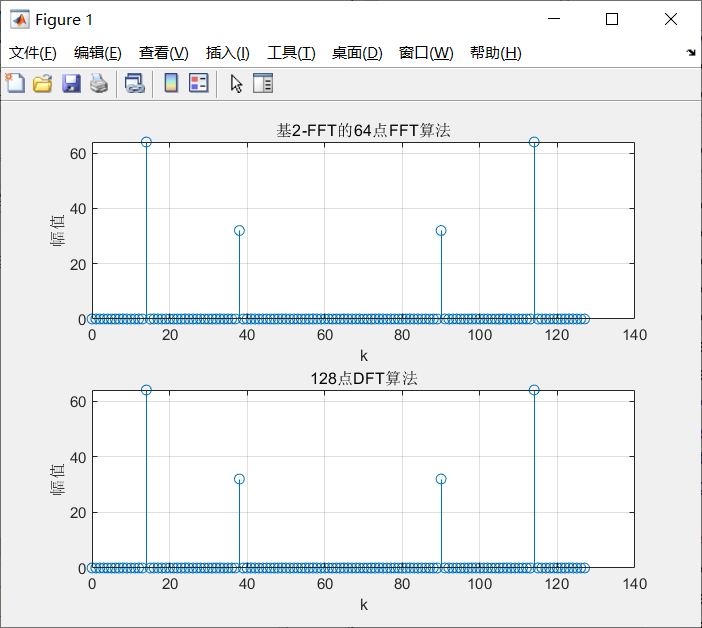
image-20211224133813396

用基2-FFT算法与直接128点DFT算法结果一致。

第2题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
clear all;
clc;
N = 64;
k = 0:N-1;
n = k;
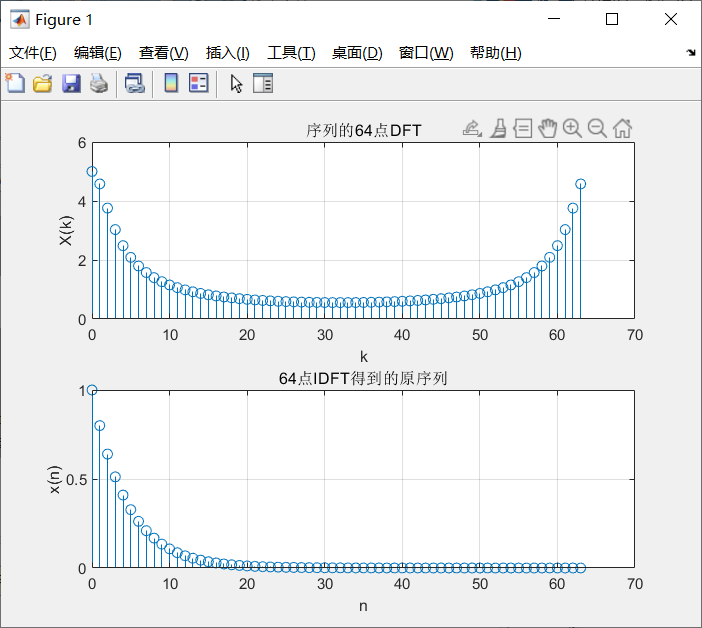
Xk = 1./(1-0.8*exp(-1i*2*pi*k/N));
xn = ifft(Xk,N);
subplot(2,1,1);
stem(k,abs(Xk));
xlabel('k');
ylabel('X(k)');
title("序列的64点DFT");
grid on;

subplot(2,1,2);
stem(n,real(xn));
xlabel('n');
ylabel('x(n)');
title("64点IDFT得到的原序列");
grid on;

输出结果：

image-20211224133949540