数字信号处理实验——实验3 离散系统的频率响应分析和零、极点分布

clear all;
clc;
syms z;
%num为分子系数
%den为分母系数
num = [0.0528,0.0797,0.1295,0.1295,0.797,0.0528];
den = [1,-1.8107,2.4947,-1,8801,0.9537,-0.2336];
subplot(1,2,1);
[Z,P,K] = tf2zp(num,den);
zplane(Z,P);
title("零极点图");
H = (0.0528+0.0797*z^-1+0.1295*z^-2+0.1295*z^-3+0.797*z^-4+0.0528*z^-5)/(1-1.8107*z^-1+2.4947*z^-2-1.8801*z^(-3)+0.9537*z^(-4));
%取w为0~pi/2的16个点
w = [pi/8,2*pi/8,3*pi/8,4*pi/8,5*pi/8,6*pi/8,7*pi/8,pi,9*pi/8,10*pi/8,11*pi/8,12*pi/8,13*pi/8,14*pi/8,15*pi/8,2*pi];
Hf = freqz(num,den,w);
Habs = abs(Hf);
subplot(1,2,2);
stem(w,Habs);
title("幅频响应");
xlabel("w");

%r为各分式的系数
%p为极点
%k为常数项
[r,p,k] = residuez(num,den)

输出：

r =

0.0159 - 0.0033i 0.0159 + 0.0033i 0.0104 - 0.0023i 0.0104 + 0.0023i -0.0005 + 0.0000i 0.0006 + 0.0000i

p =

7.2784 + 6.8733i 7.2784 - 6.8733i -6.3730 + 6.8705i -6.3730 - 6.8705i -0.0052 + 0.0000i 0.0051 + 0.0000i

k =

[ ]

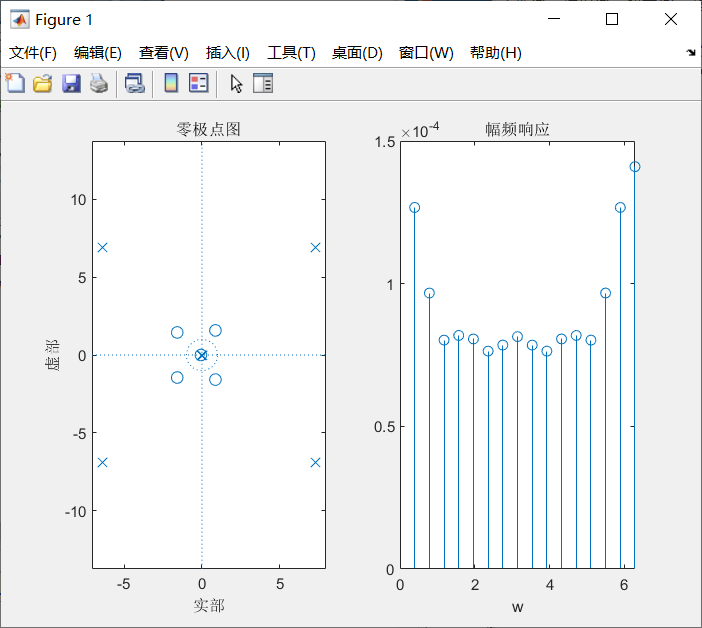
零、极点分布图和幅频响应：