一、实验目的
掌握指针变量、动态变量的含义,掌握二叉树的结构特征,以及各种存储结构的特点及适用范围,掌握指针类型描述、访问和处理二叉树的运算;
二、实验原理
参照课本p.95-107, Figure4.13-4.25;
三、实验内容
已知以二叉树表作为存储结构,写出按层次顺序遍历二叉树的算法
算法思想:本算法采用一个队列q,先将二叉树根节点入队列,然后退队列,输出该节点,若它有左子树,便将左子树根节点入队列;若有右子树,便将右子树根节点入队列,直到队列空为止。因为队列的特点是先进先出,从而达到按层次顺序遍历二叉树的目的。
四、实验要求
实现二叉树表的层次遍历算法,并给出应用。
五、实验源程序
Binary.h 头文件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #ifndef _BinaryTree_H
struct TreeNode;
typedef struct TreeNode *Position;
typedef struct TreeNode *Root;
struct Queue;
typedef struct Queue *QueueNode;
/*队列相关函数*/
QueueNode CreatQueue(); //创建队列
void EnterQueue(QueueNode A,Root T); //入队列
void OutQueue(QueueNode A); //出队列
int QueueEmpty(QueueNode A); //检查队列是否为空
/*二叉树相关函数*/
Root MakeEmpty(); //创建空树
Position Find(Root T,int X); //查找值对应的节点
Position FindMin(Root T); //查找树的最小值
Position FindMax(Root T); //查找树的最大值
Root Insert(Root T,int X); //插入值
Root Delete(Root T,int X); //删除值
void PreTraverse(Root T); //前序遍历二叉树
void MidTraverse(Root T); //中序遍历二叉树
void RearTraverse(Root T); //后序遍历二叉树
void LevelTraverse(Root T); //层次遍历二叉树
#endif // !_BinaryTree_H
|
Binary.c 主程序文件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
| #include <BinaryTree.h>
#include <stdio.h>
#include<stdlib.h>
int layer = -1;
struct Queue
{
Root data[100];
int front;
int behind;
int size;
};
struct TreeNode
{
int element;
Root left;
Root right;
};
QueueNode CreatQueue()
{
QueueNode A = (QueueNode)malloc(sizeof(struct Queue));
A->front = 0;
A->behind = 0;
A->size = 0;
printf("初始化队列成功!\n");
return A;
}
void EnterQueue(QueueNode A,Root T)
{
A->data[A->behind] = T;
A->behind++;
A->front = A->behind-1;
A->size++;
}
void OutQueue(QueueNode A)
{
for(int i =1;i<A->behind;i++)
A->data[i-1] = A->data[i];
A->size--;
A->behind--;
}
int QueueEmpty(QueueNode A)
{
return A->size == 0;
}
//创建一个空树,根的值变量为0
Root MakeEmpty()
{
Root T = (Root)malloc(sizeof(struct TreeNode));
if(T == NULL)
printf("创建新空树失败,超出内存空间!\n");
else
{
T->element = 0;
T->right = NULL;
T->left = NULL;
printf("创建空树成功!!!\n");
}
return T;
}
Root Insert(Root T, int X)
{
if(T == NULL)
{
T = (Root)malloc(sizeof(struct TreeNode));
if(T == NULL)
//若创建不成功则说明创建越界
printf("创建新树不成功,超出内存空间!");
else
{
T->element = X;
T->left = NULL;
T->right = NULL;
}
}
else if(X<T->element)
T->left = Insert(T->left, X);
else if(X>T->element)
T->right = Insert(T->right,X);
return T;
}
Root Delete(Root T,int X)
{
Root TemCell;
if(T == NULL)
{
printf("树为空!");
return NULL;
}
else if(X<T->element)
T->left = Delete(T->left, X);
else if(X>T->element)
T->right = Delete(T->right, X);
else if((T->left!=NULL)&&(T->right!=NULL))
{
TemCell = FindMin(T->right);
T->element = TemCell->element;
T->right = Delete(T->right,T->element);
}
else
{
TemCell = T;
if(T->left == NULL)
T = T->right;
else if(T->right == NULL)
T = T->left;
free(TemCell);
}
return T;
}
Position Find(Root T,int X)
{
if (T == NULL)
{
printf("不存在该数或树为空!");
return NULL;
}
if(X<T->element)
T = Find(T->left,X);
else if(X>T->element)
T = Find(T->right,X);
else
return T;
}
Position FindMin(Root T)
{
if(T!= NULL)
while(T->left!=NULL)
T = T->left;
return T;
}
Position FindMax(Root T)
{
if(T!= NULL)
while(T->right!=NULL)
T = T->right;
return T;
}
void PreTraverse(Root T)
{
if(T != NULL)
{
printf("%d\t", T->element); //访问根节点
PreTraverse(T->left); //前序遍历左子树
PreTraverse(T->right); //前序遍历右子树
}
}
void MidTraverse(Root T)
{
if(T!=NULL)
{
MidTraverse(T->left); //中序遍历左子树
printf("%d\t",T->element); //访问根节点
MidTraverse(T->right); //中序遍历右子树
}
}
void RearTraverse(Root T)
{
if(T!=NULL)
{
RearTraverse(T->left); //后序遍历左子树
RearTraverse(T->right); //后序遍历右子树
printf("%d\t",T->element); //访问根节点
}
}
void LevelTraverse(Root T)
{
QueueNode A = CreatQueue();
EnterQueue(A,T);
while(!QueueEmpty(A))
{
Root Qfront = A->data[0];
printf("%d\t",Qfront->element);
OutQueue(A);
//将出队节点的左子树根入队
if(Qfront->left)
EnterQueue(A,Qfront->left);
//将出队节点的右子树
if(Qfront->right)
EnterQueue(A,Qfront->right);
}
}
int main(void)
{
Position P;
Root T = MakeEmpty();
int n,temp,num;
if(T != NULL)
while(1)
{
printf("请选择要进行的操作:1.插入数据 2.删除数据 3.查找数据 4.查找最小数据 5.查找最大数据 6.层次遍历输出二叉树 7.前序遍历输出二叉树 8.中序遍历输出二叉树 9.后序遍历输出二叉树:\n");
scanf_s("%d", &n);
switch(n)
{
case 1:
printf("请输入要插入数据的个数:");
scanf_s("%d", &temp);
printf("\n");
for(int i=0; i<temp;i++)
{
printf("请输入要插入的数据:");
scanf_s("%d", &num);
T = Insert(T,num);
printf("\n");
}
break;
case 2:
printf("请输入你要删除的数据:");
scanf_s("%d", &num);
Delete(T,num);
printf("\n");
printf("删除成功!\n");
break;
case 3:
printf("请输入要查找的数据:");
scanf_s("%d", &num);
P = Find(T,num);
printf("\n");
if(P!=NULL)
printf("您要查找的%d在内存空间中的%d位置\n",P->element,(int)P);
break;
case 4:
P = FindMin(T);
printf("当前树的最小数据为%d\n",P->element);
break;
case 5:
P = FindMax(T);
printf("当前树的最大数据为%d\n",P->element);
break;
case 6:
printf("层次遍历数如下:\n");
LevelTraverse(T);
printf("\n");
break;
case 7:
printf("前序遍历数如下:\n");
PreTraverse(T);
printf("\n");
break;
case 8:
printf("中序遍历数如下:\n");
MidTraverse(T);
printf("\n");
break;
case 9:
printf("后序遍历数如下:\n");
RearTraverse(T);
printf("\n");
break;
}
}
}
|
六、实验结果
实验采用交互的方式,用户可以自己选择要执行的操作:
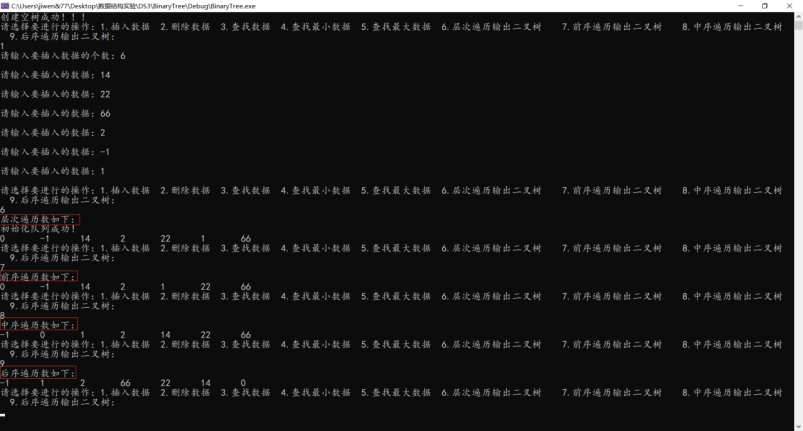
层次、前序、中序、后序遍历功能正常!

插入数据再验证功能依旧正常!
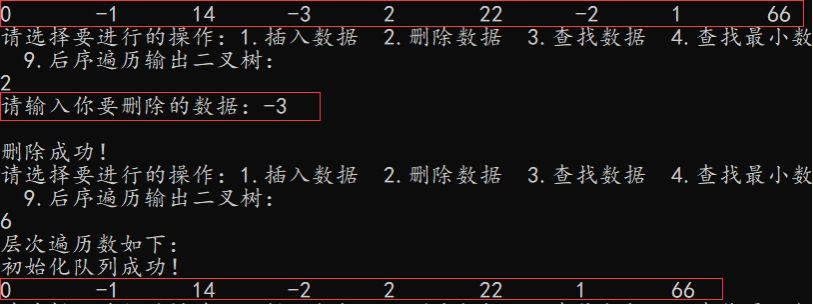
删除二叉树节点功能正常!
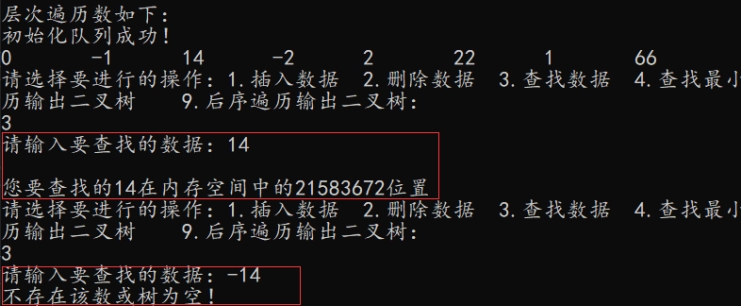
查找功能正常!
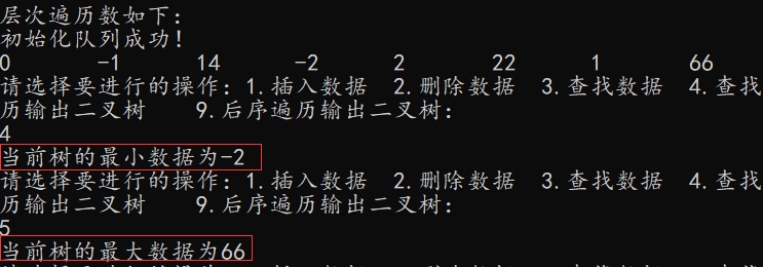
查找树最大最小值功能正常!





